Fundamentals of Waveforms

Waveforms denoted as arbitrarily varying real or complex valued functions of time. An individual waveform from an analog source should be viewed as a sample waveform from a random process. Here the focus is on ways to map deterministic waveforms to sequences and vice versa.

Introduction

Successive transmission of discrete data messages is known as digital communication.
Binary logic familiar to most electrical engineers transmits some positive voltage level for a 1 and another voltage level for a 0 inside integrated circuits. Clearly such 1/0 transmission would not pass through a linear time-invariant channel(that has the Fourier transform indicated). Instead the two modulated signals \(x_0(t) = +cos(2\pi t)\) and \(x_1(t) = −cos(2\pi t)\) (Binary Phase-Shift Keying) will easily pass through this channel and be readily distinguishable at the channel output.
Coding could change the input waveforms so as to make the decoding more effective:

For the antenna example, a real waveform at the input in the appropriate frequency band is converted by the input antenna into electromagnetic radiation, part of which is received at the receiving antenna and converted back to a waveform.
The function of a channel encoder, i.e., a modulator, is to convert the incoming sequence of binary digits into a waveform in such a way that the noise corrupted waveform at the receiver can, with high probability, be converted back into the original binary digits. This is typically done by first converting the binary sequence into a sequence of analog signals, which are then converted to a waveform.
These waveforms are a priori unknown, so much mathematical precision is necessary here.
The notation \(\{u(t) : \mathbb{R} \rightarrow \mathbb{R}/\mathbb{C}\}\) refers to a function that maps each real number \(t \in \mathbb{R}\) into a real\(/\)complex number \(u(t) \in \mathbb{R}/\mathbb{C}\).

Finite energy functions

The energy in a real or complex waveform \(u(t)\) is defined to be \(\int_{-\infty}^\infty|u(t)|^2dt\).

• The energy used over any finite interval \(T\) is limited both by regulatory agencies and by physical constraints on transmitters and antennas.
• Finite-energy waveforms have measurability properties, These finite-energy measurable functions are called \(L^2\) functions. When time-constrained, they always have Fourier series, and without a time constraint, they always have Fourier transforms.
• Perhaps the most important property, however, is that \(L^2\) functions can be treated essentially as conventional vectors.
• A major reason for restricting attention to finite-energy waveforms is that as their energy gets used up in different degrees of freedom (i.e., expansion coefficients), there is less energy available for other degrees of freedom, so that some sort of convergence must result.
• Unit impulses and constant functions are not physical waveforms, they are useful models of physical waveforms where energy is not important. However, that such waveforms can safely be limited to the finite-energy class.

Waveform Representation by Vectors

Considers the set of real-valued functions \(\{f(t)\}\) such that \(\int_0^t f^2(t)dt < \infty\) (technically known as the Hilbert space of continuous time functions and abbreviated as \(L^2[0, T]\)).
This infinite dimensional vector space has an inner product, which permits the measure of distances and angles between two different functions \(f(t)\) and \(g(t)\),

$$\langle f(t), g(t) \rangle = \int_0^T f(t) g^*(t) dt$$

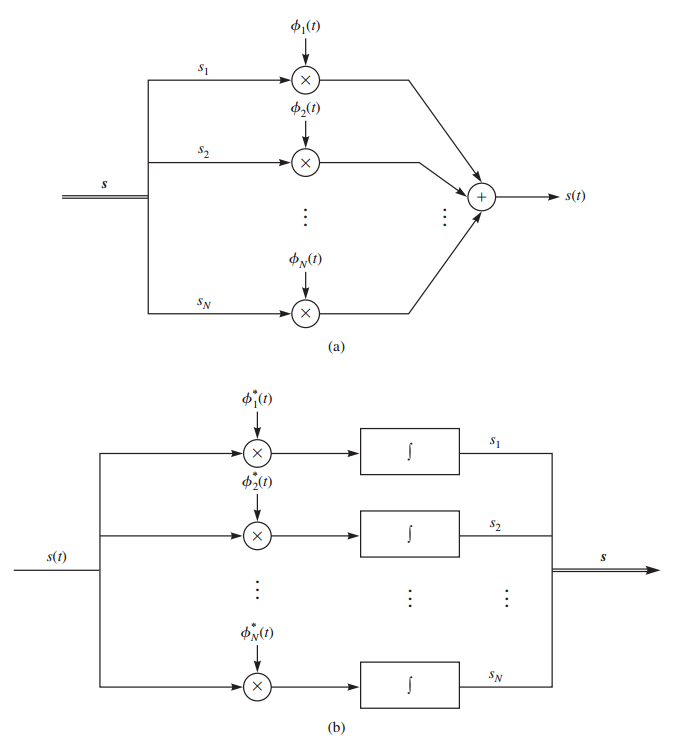
Any “well-behaved” continuous time function \(x(t)\) defined on the interval \([0, T]\) decomposes according to some set of \(N\) orthonormal basis functions \(\{\phi_i(t)\}\) as

$$x(t) = \sum\limits_{n=1}^N x_n\cdot\phi_n(t)$$

Thus the function \(x(t)\) maps to a set of \(N\) numbers {xi}, \({\bf x} = [x_1, \cdots, x_n]\).
The figure demonstrates the process of obtaining the vector equivalent from a signal (signal-to-vector mapping) and vice versa (vector-to-signal mapping).

Reference:

1. Robert G.Gallager. (2009). Principles of Digital Communication (New York: Cambridge University Press).
2. Terence Tao. (2009). Analysis I. Analysis II (Hindustan Book Agency)
3. John M. Cioffi. (2007). EE 379A Digital Communication: Signal Processing. (https://www.stanford.edu/).
4. John G. Proakis. (2008). Digital Communications, Fifth Edition. (New York: McGraw-Hill).

A good person! More about the author →