Limit and Series

The limit is a concept which on one level is quite intuitive, but to pin down rigorously turns out to be quite difficult.

Limit Notion

To get real numbers from retional numbers, that is to pass from a “discrete” system to a “continuous” one, and requires the limit notion.

Cauchy sequences of rationals

A sequence \(a_0, a_1, ...\) is \(\varepsilon\)-steady iff \(d(a_j, a_k) \le \varepsilon\) for all \(j,k\); what’s more, the sequence is eventually \(\varepsilon\)-steady iff there exists an \(N \ge 0\) such that \(d(a_j, a_k) \le \varepsilon\) for all \(j,k \ge N\).
A sequence \((a_n)_{n=0}^\infty\) of rational numbers is said to be a Cauchy sequence iff for every \(\varepsilon \gt 0\), the sequence is eventually \(\varepsilon\)-steady.

Real numbers

A real number is defined to be an object of the form \(LIM_{n\rightarrow\infty} a_n\), where \((a_n)_{n=1}^\infty\) is a Cauchy sequence of rational numbers. Two real numbers \(LIM_{n\rightarrow\infty} a_n\) and \(LIM_{n\rightarrow\infty} b_n\) are said to be equal iff \((a_n)_{n=1}^\infty\) and \((b_n)_{n=1}^\infty\) are equivalent Cauchy sequences.

Cauchy sequences of reals

Let \(\varepsilon \gt 0\) be a real number. A sequence \((a_n)_{n=m}^\infty\) starting at some integer index \(m\) is said to be eventually \(\varepsilon\)-steady iff there exists an \(N \ge m\) such that \((a_n)_{n=m}^\infty\) is \(\varepsilon\)-steady. We say that \((a_n)_{n=m}^\infty\) is a Cauchy sequence iff it is eventually \(\varepsilon\)-steady for every \(\varepsilon \gt 0\).

Convergence of sequences

Let \(\varepsilon \gt 0\) be a real number, and let \(L\) be a real number. A sequence \((a_n)_{n=1}^\infty\) of real numbers is said to be \(\varepsilon\)-close to \(L\) iff a \(n\) is \(\varepsilon\)-close to \(L\) for every \(n \ge N\), i.e., we have \(|a_n - L| \le \varepsilon\) for every \(n \ge N\). We say that a sequence \((a_n)_{n=m}^\infty\) is eventually \(\varepsilon\)-close to \(L\) iff there exists an \(N \ge m\) such that \((a_n)_{n=1}^\infty\) is \(\varepsilon\)-close to \(L\). We say that a sequence \((a_n)_{n=m}^\infty\) converges to \(L\) iff it is eventually \(\varepsilon\)-close to \(L\) for every real \(\varepsilon \gt 0\).
Convergent sequences are Cauchy.

Uniqueness of limits

Let \((a_n)_{n=m}^\infty\) be a real sequence starting at some integer index \(m\), and let \(L \neq L'\) be two distinct real numbers. Then it is not possible for \((a_n)_{n=m}^\infty\) to converge to \(L\) while also converging to \(L'\).

Limits of sequences

If a sequence \((a_n)_{n=m}^\infty\) converges to some real number \(L\), we say that \((a_n)_{n=m}^\infty\) is convergent and that its limit is \(L\); we write

$$L = \lim_{n\rightarrow\infty} a_n$$ denote this fact. If a sequence \((a_n)_{n=m}^\infty\) is not converging to any real number \(L\), we say that the sequence \((a_n)_{n=m}^\infty\) is divergent and we leave \(\lim_{n\rightarrow\infty} a_n\) an undefined.

Series

The difference between “sum” and “series” is a subtle linguistic one. Strictly speaking, a series is an expression of the form \(\sum_{i=m}^n a_i\); this series is mathematically (but not semantically) equal to a real number, which is then the sum of that series.

Absolutely convergent

We say that this series is absolutely convergent iff the series \(\sum_{(n=m)}^\infty |a_n|\) is convergent.

Fubini’s theorem for infinite sums

Let \(\{ f : \mathbb{N}\times\mathbb{N}\rightarrow\mathbb{R} \}\) be a function such that \(\sum_{(n,m)\in \mathbb{N}\times\mathbb{N}} f(n,m)\) is absolutely convergent. Then we have

$$\sum\limits_{n=0}^\infty \big( \sum\limits_{m=0}^\infty f(n,m) \big) = \sum\limits_{(n,m)\in \mathbb{N}\times\mathbb{N}} f(n,m) = \sum\limits_{(m,n)\in \mathbb{N}\times\mathbb{N}} f(n,m) = \sum\limits_{m=0}^\infty \big( \sum\limits_{n=0}^\infty f(n,m) \big)$$

In other words, we can switch the order of infinite sums provided that the entire sum is absolutely convergent.

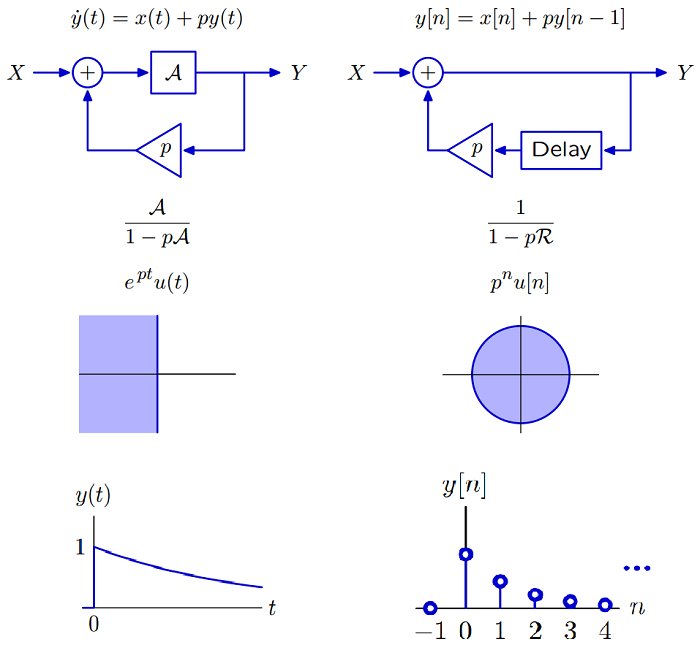
Converges Example

If the unit-impulse response or unit-sample response decays toward zero, then we say that it converges.
ROC(region of convergence) of Z transform \(X(z) = \sum\limits_{n=-\infty}^{\infty} x[n] z^{-n}\) is come from geometric series:
Let \(x\) be a complex number, then the geometricseries \(\sum_{n=0}^{\infty} x^n\) absolutely converges to \(\frac 1 {1-x}\) iff \(|x|<1\).

Reference:

1. Robert G.Gallager. (2009). Principles of Digital Communication (New York: Cambridge University Press).
2. Terence Tao. (2009). Analysis I. Analysis II (Hindustan Book Agency)
3. Dennis Freeman. (2011). 6.003 Signals and Systems. MIT OpenCourseWare (http://ocw.mit.edu/)

A good person! More about the author →