Fourier Transforms and L2 Waveforms

Posted April 01, 2017 | View revision history

The Fourier transform maps a function of time $\{u(t): R \to C\}$ into a function of frequency $\{\hat u(f) : R \to C\}$. The Fourier transform does not exist for all functions, and when the Fourier transform does exist, there is not necessarily an inverse Fourier transform. $L^2$ functions always have Fourier transforms, but only in the sense of $L^2$ equivalence.

Fourier Transform

The Fourier transform and its inverse are defined by

$$\hat u(f) = \int_{-\infty}^{\infty} u(t) e^{-2\pi ift} dt \;\;\;\; u(t) = \int_{-\infty}^{\infty} \hat u(f) e^{2\pi ift} df$$

The first integral exists for all $f$, second exists for all $t$.
If we use $\omega = 2\pi f$, these integral become

$$\hat u(\omega) = \int_{-\infty}^{\infty} u(t) e^{-i\omega t} dt \;\;\;\; u(t) = \frac 1 {2\pi} \int_{-\infty}^{\infty} \hat u(\omega) e^{i\omega t} d\omega$$

Some book denote as $\hat u(j\omega)$, that’s in the view of systems, for set $s=j\omega$ then Laplace transform becomes Fourier transform; also frequency response lives on the $j\omega$ axis of the Laplace transform.

Eigenfunctions

If the output signal $O\{ x(t)\}$ is a scalar $\lambda$ multiple of the input signal $x(t)$, we refer to the signal as an eigenfunction and the multiplier as the eigenvalue.

$$O\{ x(t)\} =\lambda x(t)$$

If $x(t) = e^{st}$ and $h(t)$ is the impulse response of LTI then $O\{ e^{st}\} = (h*x)(t) = e^{st} \int_{-\infty}^{\infty} h(\tau)e^{-s\tau} d\tau = H(s)e^{st}$.
Furthermore, the eigenvalue associated with $e^{st}$ is $H(s)$.

A Few Standard Fourier Transform Pair

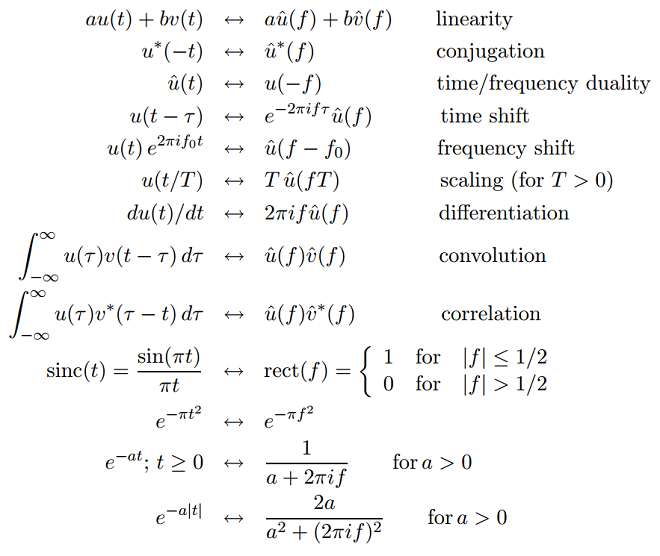Fourierpair Two useful special cases of any Fourier transform pair are:

$$u(0)=\int_{-\infty}^{\infty} \hat u(f)df \;\;\;\; \hat u(0)=\int_{-\infty}^{\infty} u(t)dt$$

Parseval’s theorem:

$$\int_{-\infty}^{\infty} u(t)v^*(t) dt = \int_{-\infty}^{\infty} \hat u(f) \hat v^*(f) df $$

Energy equation(replacing $v(t)$ by $u(t)$):

$$\int_{-\infty}^{\infty}|u(t)|^2 dt = \int_{-\infty}^{\infty} |\hat u(f)|^2 df$$

$|\hat u(f)|^2$ is called the spectral density of u(t).

Fourier transforms of $L^1$ functions

$L^1$ functions always have well-defined Fourier transforms, but the inverse transform does not always have very nice properties.
Let $\{ u(t) : \Bbb{R} \to \Bbb{C} \}$ be $L^1$. Then $\hat u(f) = \int_{-\infty}^{\infty} u(t)e^{−2\pi ift} dt$ both exists and satisfies $|\hat u(f)| \le \int |u(t)| dt$ for each $f \in \Bbb{R}$. Furthermore, $\{ \hat u(f) : \Bbb{R} \to \Bbb{C} \}$ is a continuous function of $f$.
Not enough functions are $L^1$ to provide suitable models for communication systems. For example, $sinc(t)$ is not $L^1$.
Also, functions with discontinuities cannot be Fourier transforms of $L^1$ functions.
Finally, $L^1$ functions might have infinite energy. $L^2$ functions turn out to be the “right” class.

Fourier transforms of $L^2$ functions

For any $L^2$ function $\{ u(t) : \Bbb{R} \to \Bbb{C} \}$ and any positive number $A$, define $\hat u_A(f)$ as the Fourier transform of the truncation of $u(t)$ to $[-A,A]$,

$$\hat u_A(f) = \int_{-A}^A u(t)e^{-2\pi ift} dt$$

Plancherel part 1

For any $L^2$ function $\{ u(t) : \Bbb{R} \to \Bbb{C} \}$, an $L^2$ function $\{ \hat u(f) : \Bbb{R} \to \Bbb{C} \}$ exists satisfying both

$$ \lim\limits_{A \to \infty} \int_{-\infty}^{\infty} |\hat u(f) - \hat u_A(f)|^2 df = 0$$

and the energy function.

For any $L^2$ function $\{ \hat u(f) : \Bbb{R} \to \Bbb{C} \}$ and any positive number $B$, define the inverse transform

$$u_B(t) = \int_{-B}^B \hat u(f)e^{2\pi ift} df$$

Plancherel part 2

For any $L^2$ function $\{ u(t) : \Bbb{R} \to \Bbb{C} \}$, let $\{ \hat u(f) : \Bbb{R} \to \Bbb{C} \}$ be the Fourier transform of Plancherel part 1. Then

$$ \lim\limits_{B \to \infty} \int_{-\infty}^{\infty} |u(t) - u_B(t)|^2 dt = 0$$

All $L^2$ functions have Fourier transforms in the sense of limit in mean-square equivalent ($L^2$ equivalent).

$$\hat u(f) = \underset{\rm A \to \infty}{\rm l.i.m.} \int_{-A}^A u(t)e^{-2\pi ift} dt; \;\;\;\;\; u(t) = \underset{\rm B \to \infty} {\rm l.i.m.}\int_{-B}^B \hat u(f)e^{2\pi ift} df$$

All the Fourier transform relations in the above picture except differentiation hold for all $L^2$ functions.

Reference:

Alan V.Oppenheim. Alan S.Willsky. (1998). Signals and systems 2nd ed. (China: Prentice-Hall International,Inc)
Hari Balakrishnan. George Verghese. (2012). 6.02 Introduction to EECS II: Digital Communication Systems. MIT OpenCourseWare (http://ocw.mit.edu/)
Dennis Freeman. (2011). 6.003 Signals and Systems. MIT OpenCourseWare (http://ocw.mit.edu/)
Robert Gallager. (2006). 6.450 Digital Communication. MIT OpenCourseWare (http://ocw.mit.edu/)
Robert G.Gallager. (2009). Principles of Digital Communication (New York: Cambridge University Press).
Harvey Mudd College Opencourse. E59 Administrative Information
Terence Tao. (2009). Analysis I. Analysis II (Hindustan Book Agency)

A good person! More about the author →