Aliasing and Degrees of Freedom

Posted May 31, 2017 | View revision history

An important rule of thumb used by communication engineers is that the class of real functions that are approximately baseband-limited to $W_0$ and approximately time-limited to $[−T_0/2, T_0/2]$ have about $2T_0W_0$ real degrees of freedom if $T_0W_0 >> 1$. This means that any function within that class can be specified approximately by specifying about $2T_0W_0$ real numbers as coefficients in an orthogonal expansion.

T-spaced sinc-weighted sinusoid expansion

Let $u(t) \leftrightarrow \hat u(f)$ be an arbitrary $L^2$ transform pair, and segment $\hat u(f)$ into intervals of width $2W$.

$$\hat u(f) = l.i.m.\sum\limits_k \hat v_m(f); \;\;\;\;\; \hat v_m(f) = \hat u(f)rect({f \over 2W} - m)$$

$\hat v_m(f)$ is non-zero over $[2Wm − W, 2Wm + W]$, so from the sampling theorem for $[\Delta −W, \Delta +W]$,

$$v_m(t) = \sum\limits_k v_m(kT)sinc({t \over T}-k)e^{2\pi i(m/T)(t-kT)} = \sum\limits_k v_m(kT)sinc({t \over T}-k)e^{2\pi imt/T}$$

Combining all of these frequency segments,

$$u(t) = l.i.m.\sum\limits_m v_m(t) = l.i.m.\sum\limits_{m,k} v_m(kT) \psi_{m,k}(t)$$

The doubly indexed set of orthogonal functions are the time and frequency shifts of the basic function $\psi_{0,0}(t) = sinc(t/T)$. The time shifts are in multiples of $T$ and the frequency shifts are in multiples of $1/T$.

$$\psi_{m,k}(t) = sinc({t \over T}-k)e^{2\pi imt/T}; \;\;\; m,k \in \Bbb Z$$

T-spaced truncated sinusoid expansion

Suppose that an $L^2$ waveform $\{u(t) : R \to C\}$ is segmented into segments $u_m(t)$ of duration $T$. Expressing $u(t)$ as the sum of these segments

$$u(t) = l.i.m.\sum\limits_m u_m(t); \;\;\;\;\ u_m(t) = u(t)rect({t \over T} - m)$$

For a function $\{v(t) : [\Delta −T/2, \Delta +T/2] \to \Bbb C\}$ centered around some arbitrary time $\Delta$, the shifted Fourier series over that interval is

$$v(t) = l.i.m.\sum\limits_k \hat v_k e^{2\pi ikt/T}rect({t-\Delta \over T})$$ $$\hat v_k = {1 \over T}\int_{\Delta-T/2}^{\Delta+T/2}v(t)e^{-2\pi ikt/T}dt, -\infty<k<\infty$$

Expanding each segment $u_m(t)$ by the shifted Fourier series

$$u_m(t) = l.i.m.\sum\limits_k \hat u_{k,m}e^{2\pi ikt/T}rect({t \over T} - m)$$ $$\hat u_{k,m} = {1 \over T}\int_{mT-T/2}^{mT+T/2}u_m(t)e^{-2\pi ikt/T}dt = {1 \over T}\int_{-\infty}^{\infty}u(t)e^{-2\pi ikt/T}rect({t \over T} - m)dt$$

This expands $u(t)$ as a weighted sum of doubly indexed functions

$$u(t) = l.i.m.\sum\limits_{m,k} \hat u_{k,m} \theta_{m,k}(t), \;\;\;\;\; \text{where}$$ $$\theta_{m,k}(t) = e^{2\pi ikt/T}rect({t \over T} - m)$$

Degrees of freedom

Degrees of freedom is somewhat difficult to state precisely, since time-limited functions cannot be frequency-limited and vice-versa.

Applying the sampling theorem, real (complex) functions $u(t)$ strictly baseband-limited to $W_0$ are specified by its real (complex) samples at rate $2W_0$. If the samples are nonzero only within the interval $[−T_0/2, T_0/2]$, then there are about $2T_0W_0$ nonzero samples, and these specify $u(t)$ within this class. Here a precise class of functions have been specified, but functions that are zero outside of an interval have been replaced with functions whose samples are zero outside of the interval.

Consider a large time interval $T_0$ and a baseband limited band $W_0$. There are $T0/T$ segments of duration $T$ and $W_0/2W = W_0T$ positive frequency segments. Counting negative frequencies also, there are $2T_0W_0$ time/frequency blocks and $2T_0W_0$ coefficients.

If one ignores coefficients outside of $T0$, $W0$, then the function is specified by $2T_0W_0$ complex numbers.
For real functions, it is $T_0W_0$ complex numbers.

ALIASING

The samples from different frequency slices get summed together in the samples of $u(t)$. This phenomenon is called aliasing.

A time domain approach

Suppose we approximate a function u(t) that is not quite baseband limited by the sampling expansion $s(t) \approx u(t)$.

$$s(t) = \sum\limits_k u(kT)sinc({t \over T} - k)$$ $$u(t) = l.i.m.\sum\limits_{m,k} v_m(kT)sinc({t \over T}-k)e^{2\pi imt/T}$$ $$s(kT) = u(kT) = \sum\limits_m v_m(kT) (Aliasing)$$ $$s(t) = \sum\limits_k \sum\limits_m v_m(kT)sinc({t \over T}-k)$$ $$u(t) - s(t) = \sum\limits_m \sum\limits_{m \neq 0} v_m(kT)[e^{2\pi imt/T}-1]sinc({t \over T}-k)$$

A frequency domain approach

$s(t)$ can be separated into the contribution from each frequency band as

$$s(t) = \sum\limits_m s_m(t), \;\;\;\; s_m(t) = \sum\limits_k v_m(kT)sinc({t \over T}-k)$$

Comparing $s_m(t)$ to $v_m(t)$, it is seen that

$$v_m(t) = s_m(t)e^{2\pi imt/T}, \;\;\;\; \hat s_m(f) = \hat v_m(f+{m \over T})$$

Since $\hat v_m(f) = \hat u(f) rect(fT − m)$, one sees that $\hat v_m(f+{m \over T}) = \hat u(f+{m \over T}) rect(fT)$. Thus,

$$\hat s(f) = \sum\limits_m \hat u(f+{m \over T})rect[fT]$$

Each frequency slice $\hat v_m(f)$ is shifted down to baseband in this equation, and then all these shifted frequency slices are summed together.
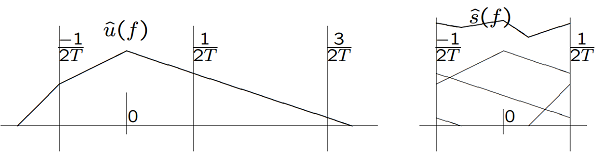
aliasing

Aliasing theorem

Let $\hat u(f)$ be $L^2$, and let $\hat u(f)$ satisfy the condition

$$\lim_{|f|\to \infty} \hat u(f)|f|^{1+\epsilon}$$

Then $\hat u(f)$ is $L^1$, and the inverse Fourier transform $u(t) = \int \hat u(f)e^{2\pi ift}df$ converges pointwise to a continuous bounded function. For any given $T > 0$, the sampling approximation $\sum_k u(kT)sinc({t \over T} − k)$ converges pointwise to a continuous bounded $L^2$ function $s(t)$. The Fourier transform of $s(t)$ satisfies

$$\hat s(f) = l.i.m. \sum\limits_m \hat u(f+{m \over T})rect[fT]$$

The condition that $\lim \hat u(f)f^{1+\epsilon} = 0$ implies that $\hat u(f)$ goes to 0 with increasing $f$ at a faster rate than $1/f$.

Without the mathematical convergence details, what the aliasing theorem says is that, corresponding to a Fourier transform pair $u(t)\leftrightarrow \hat u(f)$, there is another Fourier transform pair $s(t)$ and $\hat s(f)$; $s(t)$ is a baseband sampling expansion using the T-spaced samples of $u(t)$ and $\hat s(f)$ is the result of folding the transform $\hat u(f)$ into the band $[−W, W]$ with $W = 1/(2T)$.

Reference:

Robert Gallager. (2006). 6.450 Digital Communication. MIT OpenCourseWare (http://ocw.mit.edu/) .
Robert G.Gallager. (2009). Principles of Digital Communication (New York: Cambridge University Press).
J. M. Wozencraft and I. M. Jacobs. (1965) Principles of Communication Engineering (John Wiley and Sons, Reprinted by Waveland Press).

A good person! More about the author →