Pulse Amplitude Modulation(PAM)

PAM, or Amplitude shift keying (ASK) is a one-dimensional modulated signal set with \(M = 2^b\) signals in the constellation, the constellation is a set of real numbers. A PAM modulator is determined by the signal constellation \(\mathcal A\), the signal interval \(T\) and the real \(L^2\) modulation pulse \(p(t)\). In most cases, the pulse waveform \(p(t)\) is a baseband waveform and the resulting modulated waveform \(u(t)\) is then modulated up to some passband.

Pulse amplitude modulation

Signal constellations

PAM is modulated as \(u(t) = \sum_k u_k p(t−kT)\). A standard PAM signal set uses equi-spaced signals symmetric around 0.

$$\mathcal A = \{-d(M-1)/2, ... , -d/2, d/2, ... , d(M-1)/2 \}$$

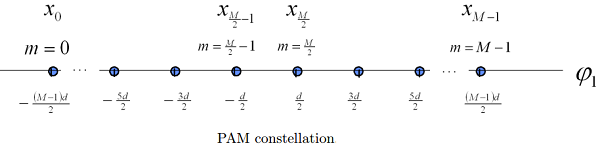
Let \(U_k\) be be a standard \(M-\)PAM random variable where the \(M\) points each have probability \(1/M\). Let \(Q\) be the quantization error for the quantizer and \(U_k\) be the quantization point, thus \(U = U_k + Q\). Observe that for each quantization point the quantization error is uniformly distributed over \([−d/2, d/2]\). This means that \(Q\) is zero mean and statistically independent of the quantization point \(U_k\). It follows that

$$E[U^2] = E[(Q + U_k)^2] = E[U_k^2] + E[Q^2] = {E[U_k^2] + d^2 \over 12}$$

For Uniform distribution \(U \sim U(a,b)\), the

$$Var(U) = {(b-a)^2 \over 12} = E[U^2] - (E[U])^2 = E[U^2] = {(dM)^2 \over 12}$$

It then follows that

$$E[U_k^2] = {d^2(M^2 - 1) \over 12} = {d^2(2^{2b} - 1) \over 12}$$

For \(b\) greater than 2, \(2^{2b} −1\) is approximately \(2^{2b}\), so we see that each unit increase in \(b\) increases \(E_s\) by a factor of 4. Thus increasing the rate \(R\) by increasing \(b\) requires impractically large energy for large \(b\).

Channel imperfections

Physical waveform channels are always subject to propagation delay, attenuation, and noise.
Estimating the fixed delay at the receiver is a significant problem called timing recovery, but is largely separable from the problem of recovering the transmitted data. This means that filtering can be non-causal, it can be incorporated into the timing recovery.
The link budget in a communication system is largely separable from other issues, so the amplitude scale at the transmitter is usually normalized to that at the receiver.
For now, we simply assume that noise can alter each received signal independently by at most a fixed amount.

Choice of the modulation pulse

The following objectives contribute to the choice of \(p(t)\), we need a compromise between time decay and bandwidth.

• \(p(t)\) must be \(0\) for \(t < −\tau\) for some finite \(\tau\).
• \(\hat p(f)\) should be essentially baseband limited to some bandwidth \(B_b\) slightly larger than \(1\over {2T}\).
• The retrieval of the sequence \(\{u_k; k \in \Bbb Z\}\) from the noisy received waveform should be simple and relatively reliable.

From Paley-Wiener theorem, functions cannot be both time and frequency limited. we will replace the first objective above with the objective of choosing \(p(t)\) to approach \(0\) rapidly as \(t \to -\infty\).

PAM demodulation

The demodulator first filters the received waveform using a filter with impulse response \(q(t)\). It then samples the output at \(T\)-spaced sample times. That is, the received filtered waveform is

$$r(t) = \int_{-\infty}^{\infty} u(\tau) q(t - \tau) d\tau = \int_{-\infty}^{\infty} \sum_k u_k p(\tau - kT) q(t - \tau) d\tau = \sum_k u_k g(t - kT)$$

where \(g(t) = p(t)*q(t)\) and the received samples are \(r(T), r(2T), ...,\).
The basis function can be any unit-energy function, but often is

$$p(t) = q(t) = {1 \over \sqrt{T}} sinc ({t \over T})$$

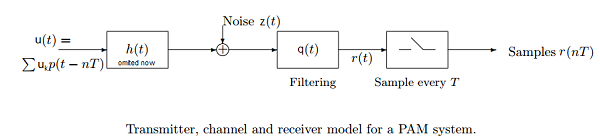
Why choose a linear filter followed by sampling seems artificial:
when noise is added, that this all makes sense as a layered solution.
Later, when channel noise is added, the individual choice of \(p(t)\) and \(q(t)\) will become important, \(q(t) = p^*(-t)\).
One PAM example is the 56 kbps voiceband modem.

Reference:

1. Robert Gallager. (2006). 6.450 Digital Communication. MIT OpenCourseWare (http://ocw.mit.edu/)
2. Robert G.Gallager. (2009). Principles of Digital Communication. (New York: Cambridge University Press).
3. Gilbert Strang. (2007 ). Computational Science and Engineering. (Wellesley-Cambridge Press).
4. John M. Cioffi. (2007). EE 379A Digital Communication: Signal Processing. (https://www.stanford.edu/).
5. John G. Proakis. (2008). Digital Communications, Fifth Edition. (New York: McGraw-Hill).

A good person! More about the author →