Nyquist Criterion

Posted October 31, 2017 | View revision history

Nyquist’s Criterion specifies the conditions on $g(t) = p(t)*p^*(−t)$ for an ISI-free channel on which a symbol-by-symbol detector is optimal.

Ideal Nyquist waveform

The demodulator first filters the received modulated waveform $u(t) = \sum_k u_k p(t-kT)$ using a filter with impulse response $q(t)$. It then samples the output at $T$-spaced sample times. That is, the received filtered waveform is

$$r(t) = \int_{-\infty}^{\infty} u(\tau) q(t - \tau) d\tau = \int_{-\infty}^{\infty} \sum_k u_k p(\tau - kT) q(t - \tau) d\tau = \sum_k u_k g(t - kT) \tag{*}$$

where $g(t) = p(t) * q(t)$, and the received samples are $r(T), r(2T), . . . ,$.
There is no intersymbol interference if $r(kT) = u_k$ for each integer $k$, and from (*) this is satisfied if $g(0) = 1$ and $g(kT) = 0$ for each nonzero integer $k$.
A waveform $g(t)$ is ideal Nyquist with period $T$ if $g(kT) = \delta(k)$.
If $g(t)$ is ideal Nyquist, then $r(kT) = u_k$ for all $k \in \Bbb Z$. If $g(t)$ is not ideal Nyquist, then $r(kT) \neq u_k$ for some $k$ and choice of ${u_k}$.

The Nyquist criterion

Let $s(t)$ be the baseband-limited waveform generated by the samples of $g(t)$,

$$s(t) = \sum_k g(kT) sinc({t \over T} − k)$$

$g(t)$ is ideal Nyquist iff $s(t) = sinc(t/T)$ i.e., iff $\hat s(f) = T rect(fT)$
From the aliasing theorem,

$$\hat s(f) = l.i.m. \sum_m \hat g(f + {m \over T}) rect(fT)$$

Nyquist criterion : Let $\hat g(f)$ be $L^2$ and satisfy the condition $\lim\limits_{|f|\to \infty} \hat g(f)|f|^{1+\varepsilon} = 0$ for some $\varepsilon > 0$. Then the inverse transform, $g(t)$, of $\hat g(f)$ is ideal Nyquist with interval $T$ if and only if $\hat g(f)$ satisfies the Nyquist criterion for $T$, defined as

$$ l.i.m. \sum_m \hat g(f + m/T) rect(fT) = T rect(fT)$$

This says that out of band frequencies can help in avoiding intersymbol interference.
The frequency $\omega = \pi / T$ or $f = 1/2T$ is called the Nyquist Frequency.

Band-edge symmetry

The choice of $\hat g(f)$ involves a tradeoff between making $\hat g(f)$ smooth, so as to avoid a slow time decay in $g(t)$, and reducing the excess of $B_b$ over the Nyquist bandwidth $W_b$. This excess is expressed as a rolloff factor, defined to be $(B_b/W_b) − 1$, usually expressed as a percentage.
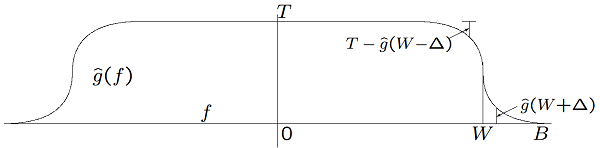
The most widely used set of functions that satisfy the Nyquist Criterion are the raised-cosine shapes, which simply rounds off the step discontinuity in $rect({f \over 2W_b})$ in such a way as to maintain the Nyquist criterion while making $\hat g(f)$ continuous with a continuous derivitive, thus guaranteeing that $g(t)$ decays asympototically with $1/t^3$. BandEdgeSymmetry

Orthonormal shifts

Orthonormal shifts theorem : Let $p(t)$ be an $L^2$ function such that $\hat g(f) = |\hat p(f)|^2$ satisfies the Nyquist criterion for $T$. Then ${p(t−kT); k \in \Bbb Z}$ is a set of orthonormal functions. Conversely, if ${p(t−kT); k \in \Bbb Z}$ is a set of orthonormal functions, then $|\hat p(f)|^2$ satisfies the Nyquist criterion.

Because of noise, we choose $| \hat p(f)| = |\hat q(f)|$. Since $\hat g(f) = \hat p(f) \hat q(f)$, this requires $\hat q(f) = \hat pˆ∗(f)$ and thus $q(t) = p^*(−t)$. This means that

$$g(t) = \int p(\tau)q(t - \tau) d\tau = \int p(\tau)p^*(\tau - t) d\tau$$

For $g(t)$ ideal Nyquist,

$$g(kT) = \int p(\tau) p^*(\tau - kT) d\tau = \begin{cases} 1 & \text { for } k = 0 \\ 0 & \text { for } k \neq 0 \end{cases}$$

This means that $\{p(t − kT); k \in \Bbb Z\}$ is an orthogonal set of functions.
Since $|\hat p(f)|^2 = \hat g(f)$, $p(t)$ is often called square root of Nyquist.
In vector terms, $u(\tau)q(kT − \tau)d\tau$ is the projection of $u$ on $p(t−kT)$. $q(t)$ is called the matched filter to p(t).

Reference:

Robert Gallager. (2006). 6.450 Digital Communication. MIT OpenCourseWare (http://ocw.mit.edu/)
Robert G.Gallager. (2009). Principles of Digital Communication. (New York: Cambridge University Press).
Gilbert Strang. (2007 ). Computational Science and Engineering. (Wellesley-Cambridge Press).
John M. Cioffi. (2007). EE 379A Digital Communication: Signal Processing. (https://www.stanford.edu/).
John G. Proakis. (2008). Digital Communications, Fifth Edition. (New York: McGraw-Hill).

A good person! More about the author →