Entropy, Relative Entropy, and Mutual Information

For any probability distribution, we define a quantity called the entropy, which has many properties that agree with the intuitive notion of what a measure of information should be. Mutual information is a measure of the amount of information one random variable contains about another. Entropy then becomes the self-information of a random variable. Mutual information is a special case of a more general quantity called relative entropy, which is a measure of the distance between two probability distributions.

What Is Information

Secrets are worth far more than silver or sapphires. —-Game of Thrones
Transform this into a mathematical statement, consider \(N\) possible events \(x_i, i = 1, 2, ... , N\), the goal is find a function \(I(x_i)\) that represents the amount of information.
\((1) p(x_i) = p(x_j) \Rightarrow I(x_i) = I(x_j)\)
\((2) p(x_i) < p(x_j) \Rightarrow I(x_i) > I(x_j)\)
\((3) p(x_i) = 1 \Rightarrow I(x_i) = 0\)
There are many functions fulfill these three requirements, e.g. \(I(x)=1/p(x) - 1\) and \(I(x)= 1/p(x) - p(x)\).
Two events are defined to be independent if \(p(x_i \cap x_j) = p(x_i)p(x_j)\).
Consider a series of experiments are conducted, assume that the two trials are independent of each other. Intuitively, it seems reasonable that if \(x_i\) occurs at one trial and \(x_j\) occurs at the next, then the total information in the two trials should be the sum of the information conveyed by receipt of \(x_i\) and \(x_j\). That is,
\((4) I(x_i \cap x_j) = I(x_i) + I(x_j)\)
Combining \((1) \thicksim (4)\), there is one and only one probability for \(I(x_i)\):

$$I(x_i) = \log ({1 \over p(x_i)}) = -\log p(x_i)$$

You have no idea, how much poetry there is in the calculation of a table of logarithms! —- Gauss
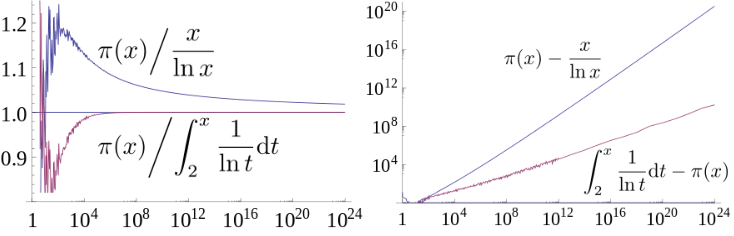
Prime number theorem: Let \(\pi(x)\) be the prime-counting function that gives the number of primes less than or equal to \(x\), for any real number \(x\).

Information Measures: Entropy

Since messages are composed of sequences of symbols, it’s important to be able to talk concretely about the average flow of information, this is called entropy.

$$H(x) = \sum_{i=1}^N p(x_i)I(x_i) = -\sum_{i=1}^N p(x_i)\log p(x_i) = E[-\log p(x_i)]$$

A concept generalizing the smallest expected number of input bits per symbol to an encoder, \(b\), is the entropy.
The entropy of a random variable(rv) can be interpreted as the “information content”, a measure of its “randomness” or “uncertainty”.
It can be easily shown that a discrete uniform distribution has the largest entropy. For instance, a uniform distribution on 4 discrete values has entropy \(H(X) = 2\) bits/symbol, this is the same as \(b\) for 4-level PAM.
The differential entropy of an analog rv can be negative and depends on the scaling of the outcomes.
The distribution with maximum differential entropy for a fixed variance \(\sigma^2\) is Gaussian.

Conditional Entropy

The definition of conditional entropy \(H(Y|X)\) is valid because conditioning \(Y\) on \(X\) moves us into a different probability space.
Remember that for any arbitrary function, \(E[f(X,Y)] = \sum_{x,y}p(x,y)f(x,y)\), so probability distributions of conditional entropy is \(p(x,y)\).

$$\begin{align} H(Y|X) &= \sum_{x \in \mathcal{X}} p(x)H(Y|X=x) \\ &= -\sum_{x \in \mathcal{X}} p(x) \sum_{y \in \mathcal{Y}} p(y|x)\log p(y|x) \\ &= -\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x,y)\log p(y|x) \\ &= -E \log p(Y|X) \end{align}$$

\(H(X|Y)\) can be interpreted as the average amount of uncertainty left in \(X\) after observing \(Y\).

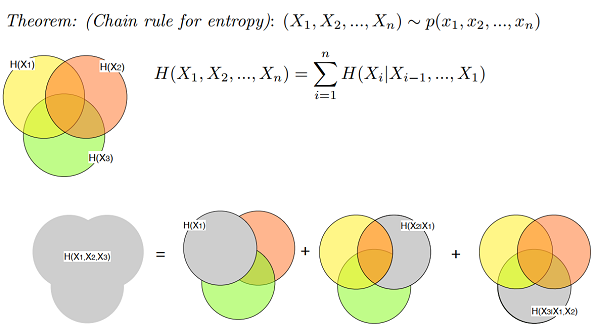
The Chain Rule for Entropy

Chain rules are important because we often encounter long chains of random variables, not just one or two.
The intuitive sense is, we observe a series of events, and each of them tells us a little bit more information.
From the product rule for probabilities, we obtain: \(\log {1 \over p(x,y)} = \log {1 \over p(x)} + \log {1 \over {p(y|x)}}\), so \(h(x,y) = h(x) + h(y|x)\).

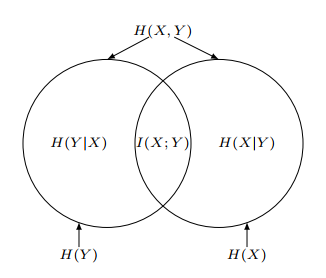
Mutual Information

Mutual information define a measure of the information that \(Y\) provides about \(X\) when \(Y\) is observed, but \(X\) is not.
It can be intuitively understood as the information that \(Y\) provides about \(X\).

$$I(X;Y) = \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y) \log {p(x,y) \over {p(x)p(y)}} = E_{p(x,y)} \log {p(X,Y) \over p(X)p(Y)}$$ $$I(X;Y) = H(X) + H(Y) − H(X,Y) = H(X) − H(X|Y)= H(Y) − H(Y|X)$$

\(I(X; X) = H(X)\) meaning that \(X\) tells us everything about itself.

Mutual information is a non-negative quantity. Relative entropy is non-negative but not a metric.

Chain Rule for Mutual Information

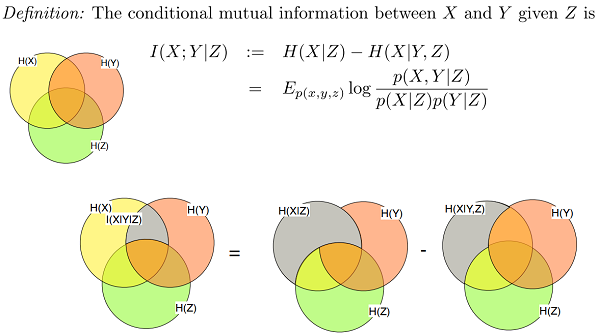
Conditional Mutual Information

Chain Rule for Mutual Information

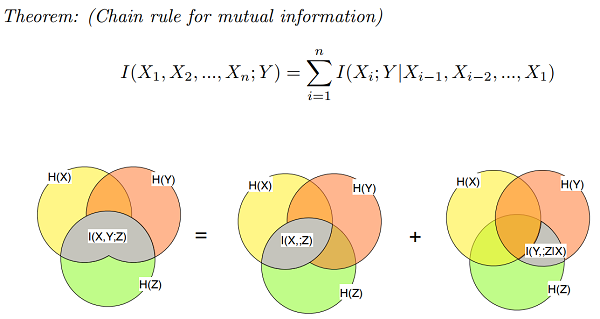
\(I(X; Y_1,Y_2) = I (X; Y_1) + I(X; Y_2|Y_1)\), where \(I(X; Y_1,Y_2)\) represents the amount of information \(Y_1\) and \(Y_2\) together give us about \(X\), and \(I(X; Y_2|Y_1)\) represents how much more information \(Y_2\) gives us about \(X\) given that we already know \(Y_1\).

Supplementary of the Reading

The textbook is Chapter 2 of “Elements of Information Theory”[ref 1].

Chain Rule

\(\eqalign { H(X, Y|Z) &= -\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}\sum_{z \in \mathcal{Z}} p(x,y,z) \log p(x,y|z) \cr &= -\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}\sum_{z \in \mathcal{Z}} p(x,y,z) \log p(x|z) - \sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}\sum_{z \in \mathcal{Z}} p(x,y,z) \log p(y|x,z) \cr &= - \sum_{x \in \mathcal{X}}\sum_{z \in \mathcal{Z}} p(x,z) \log p(x|z) - \sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}\sum_{z \in \mathcal{Z}} p(x,y,z) \log p(y|x,z) \cr &= H(X|Z) + H(Y|X,Z) }\)
\(P(X,Y|Z) = \frac{P(X,Y,Z)}{P(Z)}\)
\(P(Y|X,Z) = \frac{P(X,Y,Z)}{P(X,Z)}\)
\(P(X|Z) = \frac{P(X,Z)}{P(Z)}\)
\(P(X,Y|Z) = \frac{P(X,Y,Z)}{P(Z)} = \frac{P(X,Y,Z)}{P(X,Z)}\frac{P(X,Z)}{P(Z)} = P(Y|X,Z) P(X|Z)\)
\(H(X_1, X_2, ... , Xn) = H(X_1) + \sum\limits_{i=2}^n H(X_i | X_{i-1}, ... , X_1)\)

Chain Rule for Conditional Entropy

\(\eqalign { H(X_1, X_2, ... , X_n | Y) &= H(X_1, X_2, ... , X_n, Y) − H(Y) \cr &= H((X_1, Y), X_2, ... , X_n) − H(Y) \cr &= H(X_1, Y) +\sum\limits_{i=2}^n H(X_i|X_1, ... ,X_{i−1}, Y) − H(Y) \cr &= H(X_1|Y) + \sum\limits_{i=2}^n H(X_i|X_1, ... ,X_{i−1}, Y) \cr &= \sum\limits_{i=1}^n H(X_i|X_1, ... ,X_{i−1}, Y) }\)

Chain Rule for Mutual Information

\(I(X; Y|Z) = H(X|Z) − H(X|Y,Z)\)
\(I(X; Y,Z) - I(X; Z) = ( H(X) − H(X|Y,Z) ) - ( H(X) − H(X|Z) ) = I(X; Y|Z)\)
\(I(X; Y,Z) = I(X; Z) + I(X; Y|Z) = I(X; Y) + I(X; Z|Y)\)

Fano’s inequality

Binary entropy function: \(H(p) = −plog_2p − (1−p)log_2(1−p)\)
\(H(P_e)\) in the 2.10 of [ref 1] is usually written as
\(H(P_e) = H_b(P_e) = -P_e log(P_e) - (1-P_e) log(1-P_e)\)

Reference:

1. Thomas M. Cover, Joy A. Thomas. (2006). Elements of Information Theory. John Wiley & Sons.
2. Natasha Devroye. ECE 534: Elements of Information Theory. University of Illinois at Chicago. https://www.ece.uic.edu/ECE534 .

A good person! More about the author →