Information Theory and Communication

The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.  
    
                                                             ————C. E. SHANNON 

The characterization of the channel capacity (the logarithm of the number of distinguishable signals) as the maximum mutual information is the central and most famous success of information theory.

Discrete Memoryless Channels

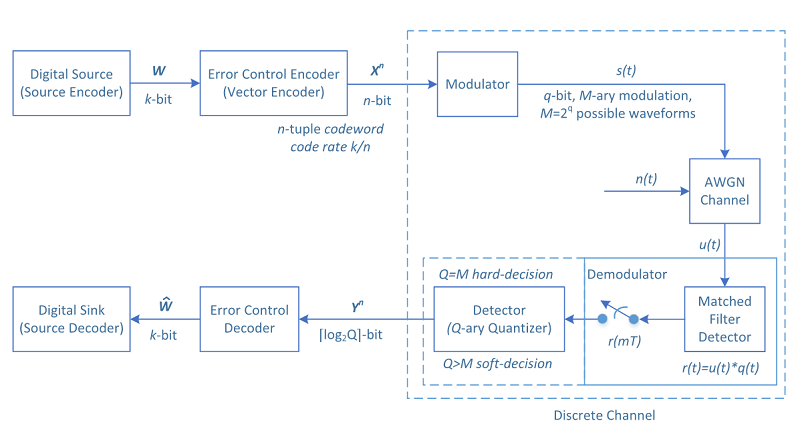
The heart of the communication problem is discrete in nature: the transmitter sends one out of a finite number of codewords and the receiver would like to figure out which codeword is transmitted.
In general, a channel is described not only by the input and output alphabets but also the probabilistic description of the outputs conditional on the inputs (the probabilistic description of the inputs is selected by the channel user).
However, it will be possible to simplify the model of uncertainty in the input data. As we have seen, the bit sequences produced by an optimal compressor have a uniform distribution (otherwise we could apply more compression to reduce the redundancy of the bits even further).
We receive a sequence of bits \((B_1, B_2, ... , B_k)\) from the compressor that is uniformly distributed on \(\{0,1\}^k\). We enumerate over all possible messages and assign each sequence a number \(W\):

$$(B_1, B_2, ... , B_k) \to W, ~~~~\text{where} ~~W \in \{1, ... , 2^k\}$$

Probability of error \(p_e = P(\hat W \neq W)\), rate \(R = k/n\).

Capacity of Binary Erasure Channel

Consider a repetition codes \(W^n, W \in \{0,1\}\), \(p_e = p^n/2\)(0,1 have a uniform distribution, all the bits get erased and a random guess makes a mistake). \(R = 1/n\) bits/symbol.

Shannon’s amazing result for BEC:
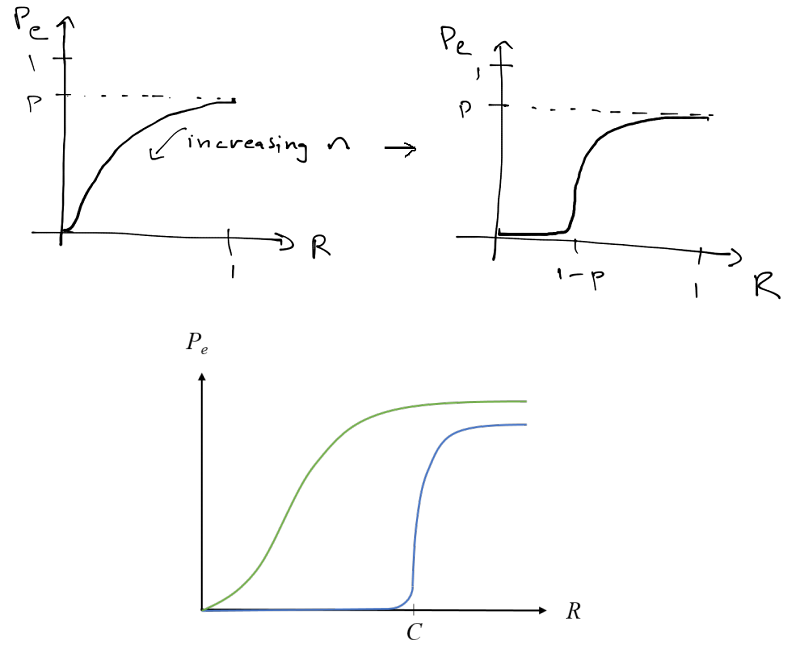
Communication is possible with arbitrarily small probability of error at positive rates, all the way up to \(C = 1 − p\).

Reference:

1. Thomas M. Cover, Joy A. Thomas. (2006). Elements of Information Theory. John Wiley & Sons.
2. David Tse. (2016). “EE376A/Stats376A: Information Theory”. Stanford Open Course (https://www.stanford.edu/) .

A good person! More about the author →