Asymptotic Equipartition Property

The asymptotic equiparitition property (AEP) is central in information theory and is the consequence of the law of large numbers.

Types of Convergence

A random variable is: a mapping from its set of sample values \(\Omega\) onto \(\cal R\).

$$X : \Omega \to \cal R$$ $$~~~~~ \xi \to X(\xi)$$

In the cases we have been discussing, \(\Omega = \cal X\) and we map onto \([0,1]\).

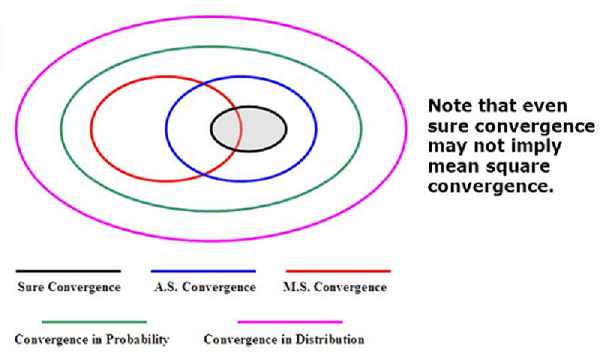
Sure Convergence

A random sequence \(X_1, . . .\) converges surely to r.v. \(X\) if \(\forall \xi \in \Omega\) the sequence \(X_n(\xi)\) converges to \(X(\xi)\) as \(n \to \infty\).

Almost Sure convergence

Also called convergence with probability 1, the random sequence converges a.s. (w.p. 1) to \(X\) if the sequence \(X_1(\xi), . . .\) converges to \(X(\xi)\) for all \(\xi\) except possibly on a set of \(\Omega\) of probability 0.

Convergence in Probability

The sequence converges in probability to \(X\) if \(\forall \epsilon > 0, \lim_{n \to \infty} P_r (|X_n - X| > \epsilon) \to 0\).

Convergence in Distribution

The sequence converges in distribution if the cumulative distribution function \(F_n(x) = P_r(X_n \le x)\) satisfies \(\lim_{n \to \infty} F_n(x) \to F_X(x)\) at all \(x\) for which \(F\) is continuous.

Venn diagram of relations among types of convergence:

Weak Law of Large Numbers

\(X_1, X_2, . . .\) are i.i.d, finite mean \(\mu\) and variance \(\sigma^2\), then \(A_X^n \to \mu\) in probability, where \(A_X^n = {X_1 + ... + X_n \over n}\)

$$Pr(|A_X^n − \mu| \ge \epsilon) \le {\sigma^2 \over {n\epsilon^2}}$$

Strong Law of Large Numbers

If \(X_i\) are i.i.d, and \(E_X (|X|) < \infty\), then

$$P_r(\lim_{n \to \infty} A_X^n = \mu) = 1$$

The difference between Strong and Weak lies in the limiting behavior of an infinite sequence of rv’s, but this difference is not relevant here.

Strong versus Weak Typicality Intuition

\(\cal X = \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\}\) with pmf \(p_X = (0.5, 0.25, 0.125, 0.125) \Rightarrow H(x) = H(0.5,0.25,0.125,0.125) = 1.75\) bit.
E.g. Sample sequence consisting of eight i.i.d samples:

• Strongly typical: all sequence with correct proportions
  \(\clubsuit\clubsuit\clubsuit\clubsuit\diamondsuit\diamondsuit\heartsuit\spadesuit \Rightarrow -\log p(x) = 14 = 8H(x)\).

• Not typical at all: \(-\log p(x) \neq nH(x)\)
  \(\spadesuit\spadesuit\spadesuit\spadesuit\spadesuit\spadesuit\spadesuit\spadesuit \Rightarrow -\log p(x) = 24 \neq 8H(x)\).

• Weekly typical: \(-\log p(x) = nH(x)\)
  \(\clubsuit\clubsuit\diamondsuit\diamondsuit\diamondsuit\diamondsuit\diamondsuit\diamondsuit \Rightarrow -\log p(x) = 14 = 8H(x)\).

Asymptotic Equipartition Propert(AEP)

APE

If \(X_1, X_2, ... , X_n {i.i.d. \atop \sim} p\), then

$$\align -{1\above n}\log p(X_1, X_2, ... , X_n) = -{1\above n}\sum_{i=1}^n\log p(X_i) \stackrel{p}{\to} -E[\log p(X)] = H(X) $$

** Typical Set**

Jointly Typical

Reference:

1. Thomas M. Cover, Joy A. Thomas. (2006). Elements of Information Theory. John Wiley & Sons.
2. Natasha Devroye. ECE 534: Elements of Information Theory. University of Illinois at Chicago. https://www.ece.uic.edu/ECE534 .

A good person! More about the author →