3GPP 5G has been focused on structured LDPC codes known as quasi-cyclic low-density parity-check (QC-LDPC) codes, which exhibit advantages over other types of LDPC codes with respect to the hardware implementations of encoding and decoding using simple shift registers and logic circuits.
5G NR QC-LDPC
Circulant Permutation Matrix
A circular permutation matrix \({\bf I}(P_{i,j})\) of size \(Z_c \times Z_c\) is obtained by circularly shifting the identity matrix \(\bf I\) of size \(Z_c \times Z_c\) to the right \(P_{i,j}\) times. We denoted this binary circulant permutation matrixas by \(Q(P_{i,j})\), considering \(Q(1)\) as an example,
$$Q(1) = \begin{bmatrix}
0 & 1 & 0 & \ldots & 0\cr
0 & 0 & 1 & \ldots & 0\cr
\vdots & \vdots & \ddots & \vdots \cr
0 & 0 & 0 & \ldots & 1\cr
1 & 0 & 0 & \ldots & 0\cr
\end{bmatrix}$$
For simple notation, \(Q(−1)\) denotes the null matrix.
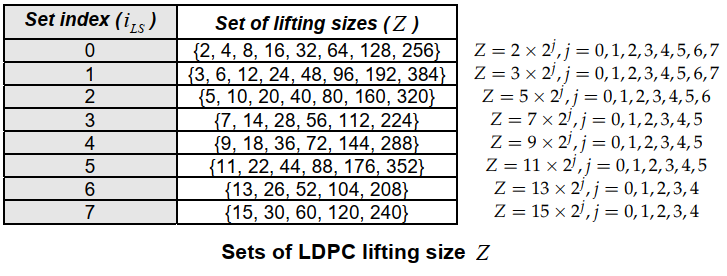
All possible lifting sizes \(Z_c\) are grouped into 8 sets, listed as \(\text{follow}^{[1]}\):
The parity-check matrix \(\bf H\) of QC-LDPC code expressed by the following \(m_b \times n_b\) array of \(Z \times Z\) circulants over \(GF(2)\):
$$H = \begin{bmatrix}
Q(P_{1,1}) & Q(P_{1,2}) & \ldots & Q(P_{1,n_b})\cr
Q(P_{2,1}) & Q(P_{2,2}) & \ldots & Q(P_{2,n_b})\cr
\vdots & \vdots & \ddots & \vdots \cr
Q(P_{m_b,1}) & Q(P_{m_b,2}) & \ldots & Q(P_{m_b,n_b})\cr
\end{bmatrix}$$
Base Graphs Characteristics
There are two rate-compatible base graphs with similar structures in 5G NR, denoted by BG1 and BG2.
BG1 is targeted for larger block lengths\((500 \le K \le 8448)\) and higher rates \((1/3 ≤ R ≤ 8/9)\).
BG2 is targeted for smaller block lengths\((40 \le K \le 2560)\) and lower rates \((1/5 \le R \le 2/3)\).
For BG1, a matrix of \(H_{BG1}\) with a size of \(m_b \times n_b(m_b = 46, n_b = 68, k_b = n_b - m_b = 22)\).
For BG2, a matrix of \(H_{BG2}\) with a size of \(m_b \times n_b(m_b = 42, n_b = 52, k_b = n_b - m_b = 10)\).
The information bit columns are \(k_b \times Z\).
The \(H \in \{H_{BG1},H_{BG2}\}\) can be partitioned into six matrices:
$$H = \begin{bmatrix}
A & B & 0\cr
C_1 & C_2 & I\cr
\end{bmatrix}$$
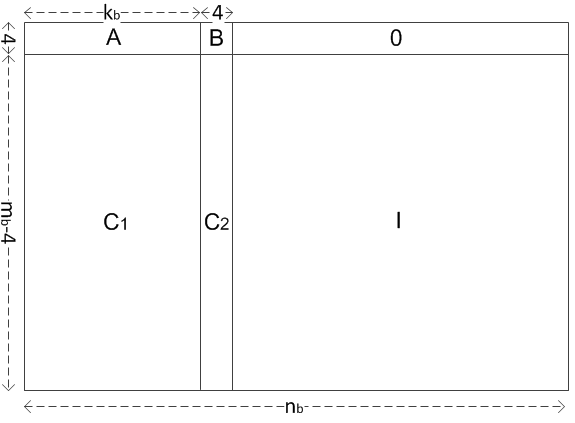
There are 8 different \(i_{LS}\) for BG1 and 8 different \(i_{LS}\) for BG2, that corresponding to 16 different \(A, C_1, C_2\).
$$A = \begin{bmatrix}
a_{1,1} & a_{1,2} & \ldots & a_{1,k_b}\cr
a_{2,1} & a_{2,2} & \ldots & a_{2,k_b}\cr
a_{3,1} & a_{3,2} & \ldots & a_{3,k_b}\cr
a_{4,1} & a_{4,2} & \ldots & a_{4,k_b}\cr
\end{bmatrix}
C_1 = \begin{bmatrix}
c_{1,1} & c_{1,2} & \ldots & c_{1,k_b}\cr
c_{2,1} & c_{2,2} & \ldots & c_{2,k_b}\cr
\vdots & \vdots & \ddots & \vdots \cr
c_{m_b-4,1} & c_{m_b-4,2} & \ldots & c_{m_b-4,k_b}\cr
\end{bmatrix}
C_2 = \begin{bmatrix}
c_{1,k_b+1} & c_{1,k_b+2} & c_{1,k_b+3} & c_{1,k_b+4}\cr
c_{2,k_b+1} & c_{2,k_b+2} & c_{1,k_b+3} & c_{2,k_b+4}\cr
\vdots & \vdots & \vdots & \vdots \cr
c_{m_b-4,k_b+1} & c_{m_b-4,k_b+2} & c_{m_b-4,k_b+3} & c_{m_b-4,k_b+4}\cr
\end{bmatrix}
$$
For simple notation, \(\{-1, 0, 1, ...\}\) denotes the \(\{Q(-1), Q(0), Q(1)...\}\).
There are 2 types of \(B \in \{H_{BG1\_B1}, H_{BG1\_B2}, H_{BG2\_B1}, H_{BG2\_B2}\}\) in both BG1 and BG2.
$$H_{BG1\_B1} = \begin{bmatrix}
1 & 0 & -1 & -1\cr
0 & 0 & 0 & -1\cr
-1 & -1 & 0 & 0\cr
1 & -1 & -1 & 0\cr
\end{bmatrix} ~~ H_{BG1\_B2} = \begin{bmatrix}
0 & 0 & -1 & -1\cr
105 & 0 & 0 & -1\cr
-1 & -1 & 0 & 0\cr
0 & -1 & -1 & 0\cr
\end{bmatrix}$$
\(H_{BG1\_B1}\) is for \(Z\) set index \(i_{LS} = (0, 1, 2, 3, 4, 5, 7)\), \(H_{BG1\_B2}\) is for \(i_{LS} = (6)\).
$$H_{BG2\_B1} = \begin{bmatrix}
0 & 0 & -1 & -1\cr
-1 & 0 & 0 & -1\cr
1 & -1 & 0 & 0\cr
0 & -1 & -1 & 0\cr
\end{bmatrix} ~~ H_{BG2\_B2} = \begin{bmatrix}
1 & 0 & -1 & -1\cr
-1 & 0 & 0 & -1\cr
0 & -1 & 0 & 0\cr
1 & -1 & -1 & 0\cr
\end{bmatrix}$$
\(H_{BG2\_B1}\) is for \(Z\) set index \(i_{LS} = (0, 1, 2, 4, 5, 6)\), \(H_{BG2\_B2}\) is for \(i_{LS} = (3, 7)\).
Encoding Algorithm
Let the codeword
$$C = [s \; p_b \; p_c] = [s_1, s_2, \ldots, s_{k_b}, p_{b_1}, p_{b_2}, p_{b_3}, p_{b_4}, p_{c_1}, p_{c_2}, \ldots, p_{c_{m_b-4}}]$$
where each element of element is a vector of length \(Z\).
The encoding of LDPC codes is carried out as follow:
$$HC^T = \begin{bmatrix}
A & B & 0\\
C_1 & C_2 & I\\
\end{bmatrix} \begin{bmatrix}
s^T\\
p_b^T\\
p_c^T\\
\end{bmatrix} = 0^T$$
that is,
$$\begin{align}
A s^T + B p_b^T &= 0^T \tag{1} \\
C_1 s^T + C_2 p_b^T + p_c^T &= 0^T \tag{2} \end{align}$$
Computation of \(p_b\)
First we determinate the \(p_b\) part from equation (1):
$$\begin{align}
H_{BG1\_B1} &: \begin{cases}
\sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1}^{(1)} + p_{b_2} = 0\\
\sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_1} + p_{b_2} + p_{b_3} = 0\\
\sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_3} + p_{b_4} = 0 \\
\sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1}^{(1)} + p_{b_4} = 0
\end{cases};~~~~~~
H_{BG1\_B2} : \begin{cases}
\sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1} + p_{b_2} = 0\\
\sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_1}^{(105~mod~Z)} + p_{b_2} + p_{b_3} = 0\\
\sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_3} + p_{b_4} = 0\\
\sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1} + p_{b_4} = 0
\end{cases};\\ \\
H_{BG2\_B1} &: \begin{cases}
\sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1} + p_{b_2} = 0\\
\sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_2} + p_{b_3} = 0\\
\sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_1}^{(1)} + p_{b_3} + p_{b_4} = 0\\
\sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1} + p_{b_4} = 0
\end{cases};~~~~~~
H_{BG2\_B2} : \begin{cases}
\sum\limits_{j=1}^{k_b}a_{1,j}s_j + p_{b_1}^{(1)} + p_{b_2} = 0\\
\sum\limits_{j=1}^{k_b}a_{2,j}s_j + p_{b_2} + p_{b_3} = 0\\
\sum\limits_{j=1}^{k_b}a_{3,j}s_j + p_{b_1} + p_{b_3} + p_{b_4} = 0\\
\sum\limits_{j=1}^{k_b}a_{4,j}s_j + p_{b_1}^{(1)} + p_{b_4} = 0
\end{cases}.
\end{align}$$
where \(p_{b_1}^{(\alpha)}\) denotes the \(\alpha^{th}\) right cyclic shifted version of \(p_{b_1}\) for \(0 ≤ \alpha ≤ Z\).
Based on the definition below,
$$\lambda_i = \sum\limits_{j=1}^{k_b}a_{i,j}s_j; ~~ i = 1, 2, 3, 4$$.
the following can be obtained:
$$\begin{align}
H_{BG1\_B1} &: \begin{cases}
p_{b_1} = \sum\limits_{i=1}^{4} \lambda_i\\
p_{b_2} = \lambda_1 + p_{b_1}^{(1)}\\
p_{b_4} = \lambda_4 + p_{b_1}^{(1)}\\
p_{b_3} = \lambda_3 + p_{b_4}
\end{cases};~~~~~~
H_{BG1\_B2} : \begin{cases}
p_{b_1}^{(105~mod~Z)} = \sum\limits_{i=1}^{4} \lambda_i \to p_{b_1}\\
p_{b_2} = \lambda_1 + p_{b_1}\\
p_{b_4} = \lambda_4 + p_{b_1}\\
p_{b_3} = \lambda_3 + p_{b_4}
\end{cases};\\ \\
H_{BG2\_B1} &: \begin{cases}
p_{b_1}^{(1)} = \sum\limits_{i=1}^{4} \lambda_i \to p_{b_1}\\
p_{b_2} = \lambda_1 + p_{b_1}\\
p_{b_3} = \lambda_2 + p_{b_2}\\
p_{b_4} = \lambda_4 + p_{b_1}
\end{cases};~~~~~~
H_{BG2\_B2} : \begin{cases}
p_{b_1} = \sum\limits_{i=1}^{4} \lambda_i\\
p_{b_2} = \lambda_1 + p_{b_1}^{(1)}\\
p_{b_3} = \lambda_2 + p_{b_2}\\
p_{b_4} = \lambda_3 + p_{b_1}^{(1)}
\end{cases}.
\end{align}$$
Computation of \(p_c\)
Secondly, the \(p_c\) can be easily determined based on equation (2):
$$p_{c_i} = \sum\limits_{j=1}^{k_b}c_{i,j}s_j + \sum\limits_{j=1}^4 c_{i,k_b+j}p_{b_j},~~i=1,2,\ldots, m_b-4$$.
Systematic Bit Puncturing
5G NR directly delete the first \(2 \times Z\) systematic bits. Here ignore the procedures of CRC, rate-matching, HARQ and so on which included in a complete channel coding link.
Reference:
- 3GPP TS 38.212. NR; Multiplexing and channel coding. 3rd Generation Partnership Project. www.3gpp.org.
- Tram Thi Bao Nguyen, Tuy Nguyen Tan, Hanho Lee. Efficient QC-LDPC Encoder for 5G New Radio. www.mdpi.com.

